Linear Predictive Coding (LPC)
Introducing Remarks
In Speech Coding the properties of speech have to be considered (unlike channel coding)
For telephone applications the speech signal has to be re-synthesized (unlike speech recognition)
Frames with a length of 10-30ms are considered
The signal is considered stationary within a frame
The LPC coefficients are calculated for each such frame
The synthesized signal can be re-used
Analysis-by-Synthesis sytem
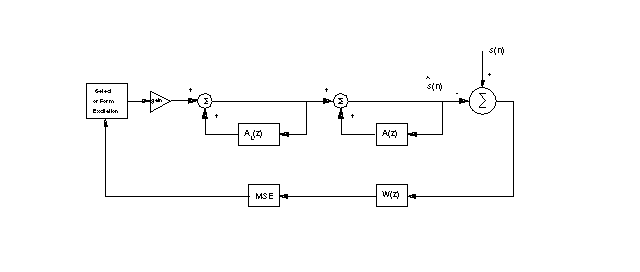
The Analysis-by-Synthesis System
A short-term LP synthesis filter representing spectral information of the speech signal
A long-term LP synthesis filter representing the pitch structure (optional)
A perceptual weighting filter, shaping the error in such a way that the quantization noise is masked by high-energy formants
Mean Squared Error (MSE) which minimizes the error signal
An excitation source, which is selected according to the error signal
The excitation is either white noise (unvoiced) or a uniform sample train (voiced)
Assume that q=0 ( autoregressive or AR model), i.e. any zeros are ignored, since they only add linear phase
Speech s(n) is filtered by an invers or predictor filter of an all-pole H(z)
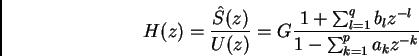 (1)
(1)
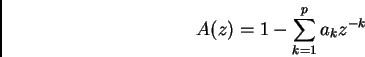 (2)
(2)
and the output e(n) is called error or risidual signal
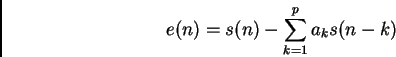 (3)
(3)
Least-Squares Autocorrelation Method
The classical least-squares method minimizes the mean energy in the error signal over a frame of speech data
The speech signal is multiplied by a Hamming window (or similar window)
 (4)
(4)
The LPC coefficients describe a smoothed average of the signal
Let E be the error energy
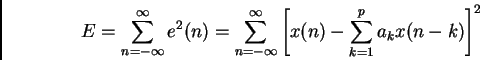 (5)
(5)
where e(n) is the risidual corresponding to the windowed signal x(n)
The coefficients are found by partial differentiations
 (6)
(6)
This yields p linear equations in p unknown filter coefficients
Finally we receive the minimum risidual energy or prediction energy for a p-pole model
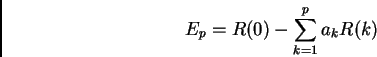 (7)
(7)
Problems
There are only two options for excitation which lowers speech quality
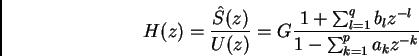 (1)
(1)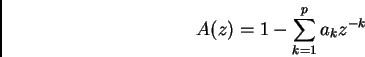 (2)
(2)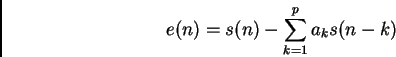 (3)
(3) (4)
(4)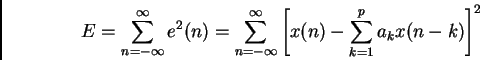 (5)
(5) (6)
(6)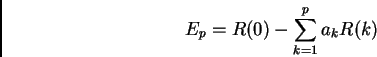 (7)
(7)